10. 优化算法
10.1. 可视化
等高线
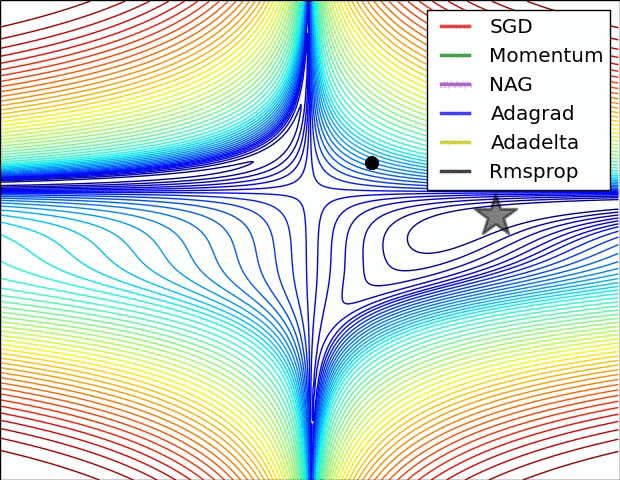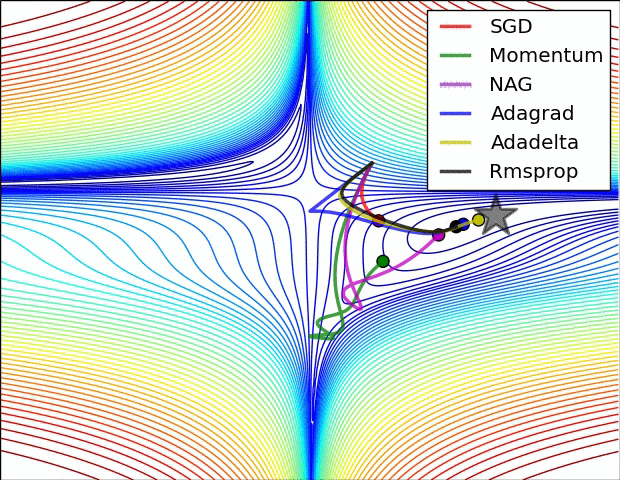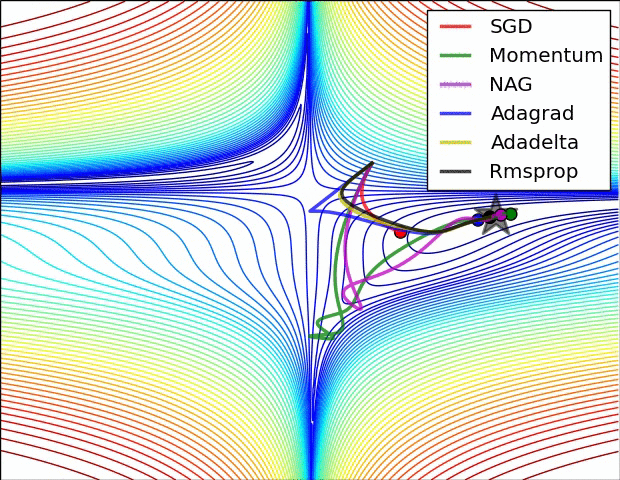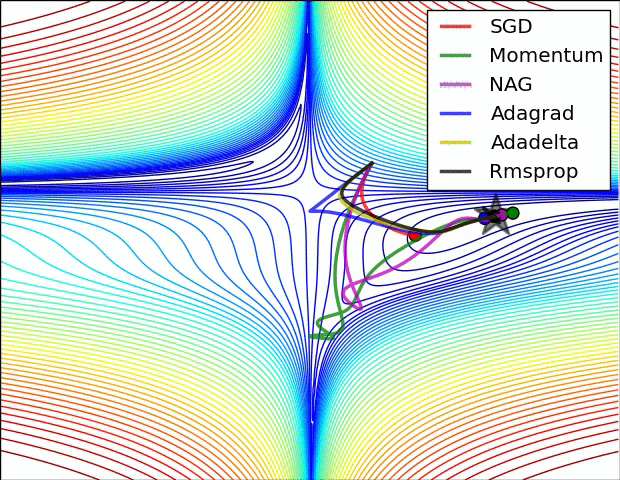
鞍点
不是局部极值点的驻点(一阶梯度为零)。在鞍点处,Hessian 是不定矩阵(Indefinite):既不是半正定,也不是半负定。判断鞍点的充分条件:Hessian 矩阵同时具有正、负特征值。
双曲抛物线(马鞍面) \(z = \frac{x^2}{a^2} - \frac{y^2}{b^2}\) 的鞍点在 \((0,0)\) 。
\(y = x^3\) 的鞍点在 \((0,0)\) 。
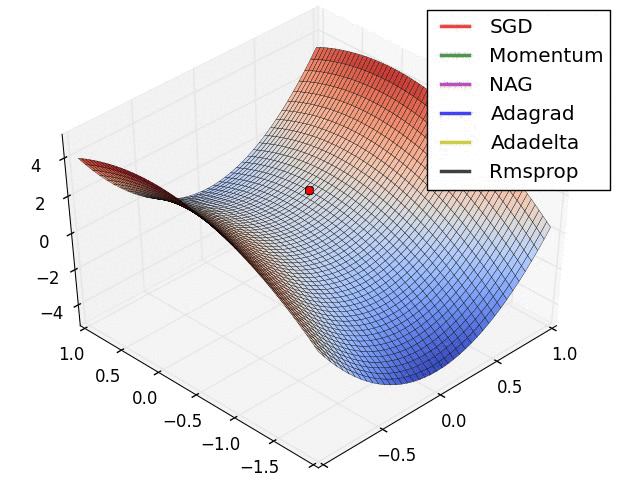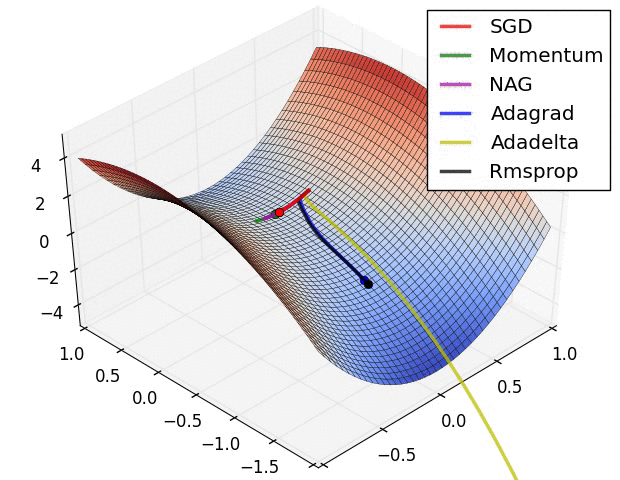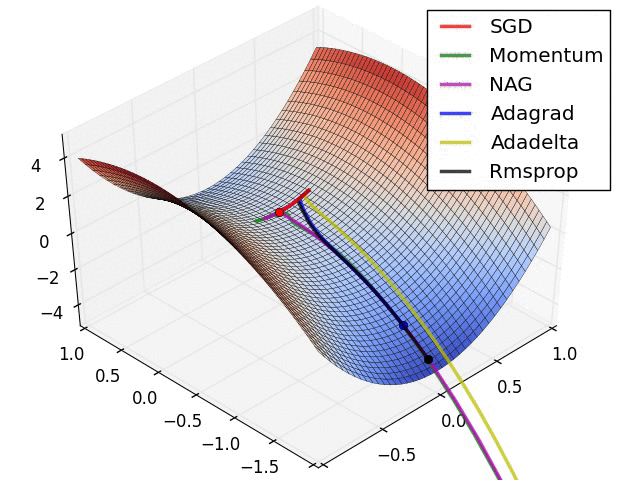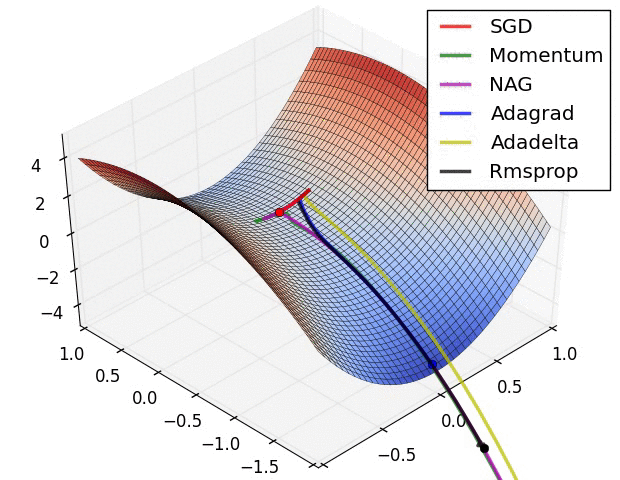
10.2. SGD
这里 SGD 指小批量梯度下降算法。
小批量损失:\(\mathcal{L}\) ,学习率:\(\eta\) ,Hadamard 积:\(\odot\) 。
\[\begin{split}g & \leftarrow \nabla_{\theta} \mathcal{L} (\theta; x^{(i:i+n)}; y^{(i:i+n)}) &\ [\text{计算梯度}] \\
\theta & \leftarrow \theta - \eta g &\ [\text{参数更新}]\end{split}\]
- 特点
相比于单样本 SGD,可以降低参数更新时的方差,收敛更稳定;可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算
不能保证很好的收敛性:如果选择的太小,收敛速度会很慢;如果太大,损失函数就会在极小值处不停地震荡甚至偏离;容易困在鞍点。
选择合适的学习率比较困难:对所有的参数更新使用同样的学习率。对于稀疏数据或者特征,有时我们可能想更快更新对应于不经常出现的特征的参数,对于常出现的特征更新慢一些。
10.3. Momentum
\[\begin{split}v & \leftarrow \gamma v - \eta \nabla_{\theta} \mathcal{L}(\theta) &\ [\text{速度更新}] \\
\theta & \leftarrow \theta + v &\ [\text{参数更新}]\end{split}\]
动量(Momentum)方法旨在加速学习,特别是处理高曲率、小但一致的梯度,或是带噪声的梯度。动量算法积累了之前梯度指数级衰减的移动平均,并且沿该方向继续移动。
当许多连续的梯度指向相同的方向时,步长最大。
- 特点
-
10.4. Adagrad
\[\begin{split}g & \leftarrow \nabla_{\theta} \mathcal{L}(\theta) &\ [\text{计算梯度}] \\
r & \leftarrow r + g \odot g &\ [\text{累计平方梯度}] \\
\Delta \theta & \leftarrow - \frac{\eta}{\sqrt{r+\epsilon}} \odot g &\ [\text{梯度除以累计平方梯度的平方根}] \\
\theta & \leftarrow \theta + \Delta \theta &\ [\text{参数更新}]\end{split}\]
- 特点
-
10.5. Adadelta
\[\begin{split}g & \leftarrow \nabla_{\theta} \mathcal{L}(\theta) &\ [\text{计算梯度}] \\
E[g^2] & \leftarrow \gamma E[g^2] + (1 - \gamma) g \odot g &\ [\text{累计平方梯度:指数衰减平均}] \\
RMS[g] & \leftarrow \sqrt{E[g^2] + \epsilon} &\ [\text{梯度均方根}] \\
E[\Delta \theta^2] & \leftarrow \gamma E[\Delta \theta^2] + (1 - \gamma) \Delta \theta \odot \Delta \theta &\ [\text{平方参数增量平滑}] \\
RMS[\Delta \theta] & \leftarrow \sqrt{E[\Delta \theta^2] + \epsilon} &\ [\text{参数增量均方根}] \\
\Delta \theta & \leftarrow - \frac{RMS[\Delta \theta]}{RMS[g]} \odot g &\ [\text{参数增量}] \\
\theta & \leftarrow \theta + \Delta \theta &\ [\text{参数更新}]\end{split}\]
Adadelta 是 Adagrad 的改进。
- 特点
-
10.6. RMSprop
\[\begin{split}g & \leftarrow \nabla_{\theta} \mathcal{L}(\theta) &\ [\text{计算梯度}] \\
r & \leftarrow \gamma r + (1 - \gamma) g \odot g &\ [\text{累计平方梯度:指数衰减平均}] \\
\Delta \theta & \leftarrow - \frac{\eta}{\sqrt{r+\epsilon}} \odot g &\ [\text{参数增量}] \\
\theta & \leftarrow \theta + \Delta \theta &\ [\text{参数更新}]\end{split}\]
RMSprop 趋于 Adagrad 和 Adadelta 之间。
- 特点
-
10.7. Adam
\[\begin{split}g & \leftarrow \nabla_{\theta} \mathcal{L}(\theta) &\ [\text{计算梯度}] \\
t & \leftarrow t + 1 &\ [\text{迭代次数}] \\
m & \leftarrow \beta_1 m + (1 - \beta_1) g &\ [\text{有偏一阶矩}] \\
n & \leftarrow \beta_1 n + (1 - \beta_2) g \odot g &\ [\text{有偏二阶矩}] \\
\hat{m} & \leftarrow \frac{m}{1 - \beta_1^t} &\ [\text{修正一阶矩}] \\
\hat{n} & \leftarrow \frac{n}{1 - \beta_2^t} &\ [\text{修正二阶矩}] \\
\Delta \theta & \leftarrow - \eta \frac{\hat{m}}{\sqrt{\hat{n}+\epsilon}} \odot g &\ [\text{参数增量}] \\
\theta & \leftarrow \theta + \Delta \theta &\ [\text{参数更新}]\end{split}\]
相当于 RMSprop + Momentum。
- 特点
-
10.8. 参考资料
An overview of gradient descent optimization algorithms
深度学习——优化器算法Optimizer详解
深度学习——优化器算法Optimizer详解
An overview of gradient descent optimization algorithms
Saddle point

