7. Batch Normalization
上标 \((k)\) 表示向量第 \(k\) 维。
随着网络深度加深或者在训练过程中,神经元激活值的分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往激活函数函数的取值区间的上下限两端靠近(饱和), 导致反向传播时低层神经网络的梯度消失。这是训练深层神经网络收敛越来越慢的本质原因。
BN 通过一定的规范化手段,把每层神经网络任意神经元的激活值的分布强行拉回到 均值为 0 方差为 1 的标准正态分布 ,其实就是把越来越偏的分布强制拉回比较标准的分布,这样使得激活值落在激活函数的线性区域(0 附近)。 这样避免了梯度消失,梯度变大意味着学习收敛速度快,能大大加快训练速度。
BN 一般用在全连接层或卷积层之后,激活函数之前。
7.1. 加速训练
增大学习率 。由于网络参数不断更新,导致各层输入的分布不断变化,导致往往需要使用较小的学习率,并精心设计参数初始化。使用 BN 进行归一化之后,各层输入的分布相同,因此可以使用更大的学习率更快地收敛,并降低网络对初始化的依赖。
移除 Dropout 。进行 BN 之后,各样本的 Feature Map 已经融合了一个 batch 之中其他样本的特性(均值,方差),因此单一样本的影响变小,网络更好学习整体的规律,有效地减小了过拟合的可能性( BN 提供了正则化的作用)。
减小 \(L_2\) 正则化损失的权重 。
加速学习率衰减 。
7.2. BN 消除
如果在训练过程中,网络发现这种 Normalization 是多余的,可以通过学习使得:
从而消除 BN 的作用。
7.3. 训练与测试
训练
训练过程中,均值与方差是在每一个 batch 中分别计算得到的。
学习的参数为:
其中 \(C\) 是通道数(Channel)。
测试
测试(Inference)过程中的均值和方差不再是在每一个测试 batch 中计算得到,而是使用由训练集得到的全局统计量。因此,训练过程中需要记录每个 batch 的均值和方差。
测试时使用的全局统计量如下(省略维度上标):
而实际实现过程中,一般使用指数加权平均(Exponentially Weighted Averges,也称“移动平均”)来获得全局统计量,即在训练过程中使用下式更新全局统计量:
7.4. 缺点
BN 统计均值、方差与 batch size 有关,batch size 太小会导致性能变差。而某些任务受内存限制,batch size 难以设置很大,因此 BN 作用难以显现。 这时候出现了Group Normalization。
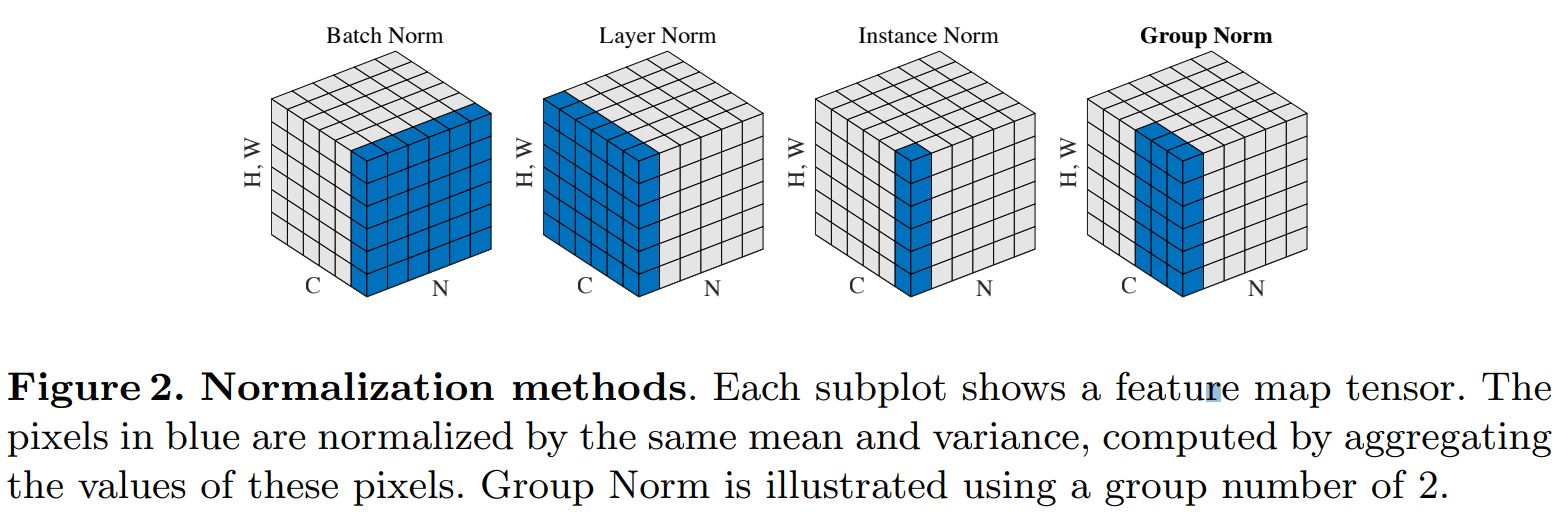
7.5. 梯度推导
前向传播
设 \(\hat{x}_i = f(x_i, \mu_B, \sigma_B^2)\) 。
反向传播
\(\gamma,\ \beta\)
\[\begin{split}\frac{\partial{\mathcal{L}}}{\partial{\gamma}} &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{y_i}} \frac{\partial{y_i}}{\gamma} = \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{y_i}} \hat{x}_i \\ \frac{\partial{\mathcal{L}}}{\partial{\beta}} &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{y_i}} \frac{\partial{y_i}}{\beta} = \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{y_i}}\end{split}\]\(\hat{x}_i\)
\[\frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} = \frac{\partial{\mathcal{L}}}{\partial{y_i}} \frac{\partial{y_i}}{\partial{\hat{x}_i}} = \frac{\partial{\mathcal{L}}}{\partial{y_i}} \cdot \gamma\]\(\sigma_B^2,\ \mu_B\)
\[\begin{split}\frac{\partial{\mathcal{L}}}{\partial{\sigma_B^2}} &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} \frac{\partial{\hat{x}_i}}{\partial{\sigma_B^2}} \\ &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} \cdot (x_i - \mu_B) \cdot \left( -\frac{1}{2} (\sigma_B^2 + \epsilon)^{-\frac{3}{2}} \right) \\ \frac{\partial{\mathcal{L}}}{\partial{\mu_B}} &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} \frac{\partial{\hat{x}_i}}{\partial{\mu_B}} \\ &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} \left( \frac{\partial{f}}{\partial{\mu_B}} + \frac{\partial{f}}{\partial{\sigma_B^2}}\frac{\partial{\sigma_B^2}}{\partial{\mu_B}} \right) \\ &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} \cdot \left( -\frac{1}{\sqrt{\sigma_B^2 + \epsilon}} \right) + \frac{\partial{\mathcal{L}}}{\partial{\sigma_B^2}} \cdot \left( - \frac{2}{m} \sum_{i=1}^m (x_i - \mu_B) \right)\end{split}\]\(x_i\)
\[\begin{split}\frac{\partial{\mathcal{L}}}{\partial{x_i}} &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} \frac{\partial{\hat{x}_i}}{\partial{x_i}} \\ &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} \left( \frac{\partial{f}}{\partial{x_i}} + \frac{\partial{f}}{\partial{\mu_B}}\frac{\partial{\mu_B}}{\partial{x_i}} + \frac{\partial{f}}{\partial{\sigma_B^2}}\frac{\partial{\sigma_B^2}}{\partial{x_i}} \right) \\ &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} \left( \frac{1}{\sqrt{\sigma_B^2 + \epsilon}} + \frac{\partial{f}}{\partial{\mu_B}} \cdot \frac{1}{m} + \frac{\partial{f}}{\partial{\sigma_B^2}} \cdot \frac{2}{m} (x_i - \mu_B) \right) \\ &=\ \sum_{i=1}^m \frac{\partial{\mathcal{L}}}{\partial{\hat{x}_i}} \cdot \frac{1}{\sqrt{\sigma_B^2 + \epsilon}} + \frac{\partial{\mathcal{L}}}{\partial{\mu_B}} \cdot \frac{1}{m} + \frac{\partial{\mathcal{L}}}{\partial{\sigma_B^2}} \cdot \frac{2}{m} (x_i - \mu_B)\end{split}\]
7.6. 代码实现
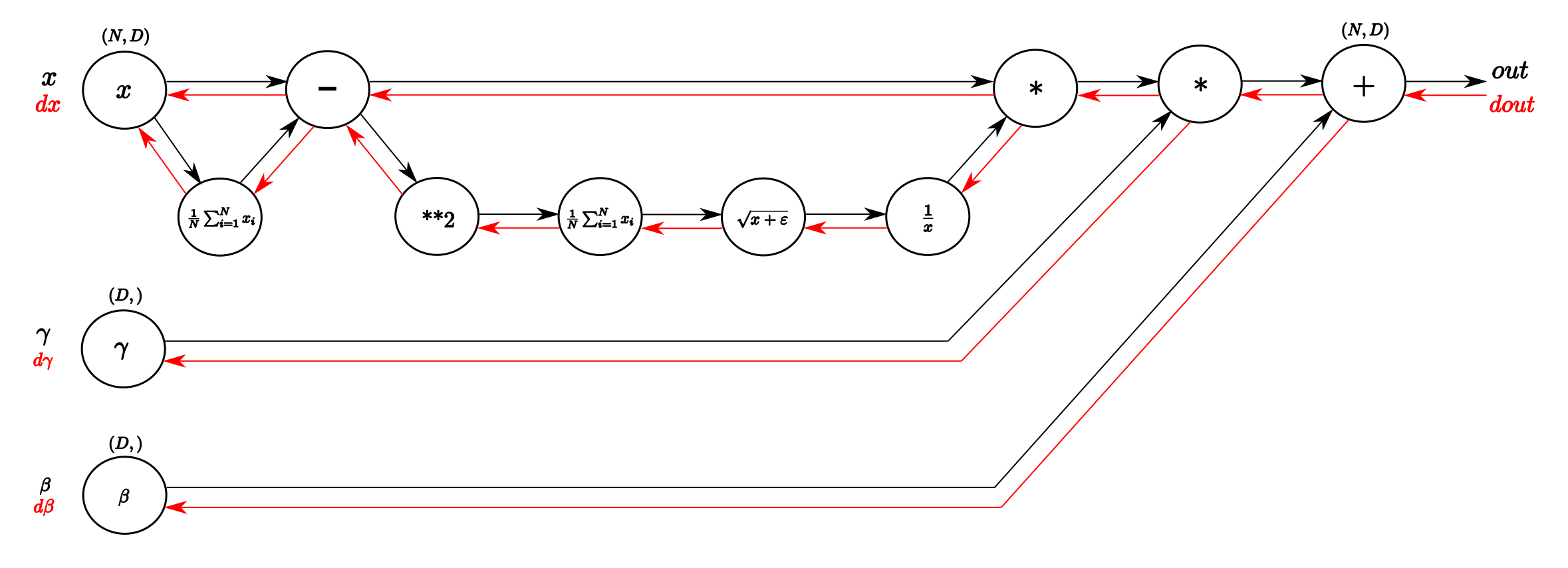
梯度回传过程中,参数及其梯度保持维度一致。
前向传播
1def batchnorm_forward(x, gamma, beta, eps):
2
3 M, D = x.shape
4
5 #step1: calculate mean
6 mu = 1. / M * np.sum(x, axis=0)
7
8 #step2: subtract mean vector of every trainings example
9 xmu = x - mu
10
11 #step3: following the lower branch - calculation denominator
12 sq = xmu ** 2
13
14 #step4: calculate variance
15 var = 1. / M * np.sum(sq, axis=0)
16
17 #step5: add eps for numerical stability, then sqrt
18 sqrtvar = np.sqrt(var + eps)
19
20 #step6: invert sqrtwar
21 ivar = 1. / sqrtvar
22
23 #step7: execute normalization (!! element-wise product !!)
24 xhat = xmu * ivar
25
26 #step8: Nor the two transformation steps (!! element-wise product !!)
27 gammax = gamma * xhat
28
29 #step9
30 out = gammax + beta
31
32 cache = (xhat, gamma, xmu, ivar, sqrtvar, var, eps)
33
34 return out, cache
反向传播
1def batchnorm_forward(dout, cache):
2
3 xhat, gamma, xmu, ivar, sqrtvar, var, eps = cache
4
5 M, D = dout.shape
6
7 #step9
8 dgamma = np.sum(dout * xhat, axis=0)
9 dbeta = np.sum(dout, axis=0)
10
11 #step8
12 dxhat = dout * gamma
13
14 #step7
15 divar = np.sum(dxhat * xmu, axis=0)
16 dxmu1 = dxhat * ivar
17
18 #step6
19 dsqrtvar = -1. / (sqrtvar ** 2) * divar
20
21 #step5
22 dvar = 1. / 2 * (1. / np.sqrt(var+eps)) * dsqrtvar
23
24 #step4
25 dsq = 1. / M * np.ones((M, D)) * dvar
26
27 #step3
28 dxmu2 = 2 * xmu * dsq
29
30 #step2
31 dxmu = dxmu1 + dxmu2
32 dmu = -1 * np.sum(dxmu, axis=0)
33 dx1 = dxmu
34
35 #step1
36 dx2 = 1. / M * np.ones((M, D)) * dmu
37
38 #step0
39 dx = dx1 + dx2
40
41 return dx, dgamma, dbeta
7.7. 参考资料
Batch Normalization
Group Normalization
深入理解Batch Normalization批标准化
Batch Normalization 学习笔记
Batch Normalization梯度反向传播推导
Understanding the backward pass through Batch Normalization Layer