6. 激活函数

神经网络引入激活函数（Activation Function）主要是为了增强网络的非线性，提升网络的拟合能力和学习能力。激活函数有以下几个性质：

  • 非线性

  • 可微性

  • 单调性：保证单层网络是凸函数

下面介绍 sigmoid 、 tanh 以及 relu 。

6.1. sigmoid

sigmoid 函数的数学表达式如下：

\[\sigma(z) = \frac{1}{1 + e^{-z}}.\]

其导数具有如下性质：

\[\sigma^\prime(z) = \sigma(z)(1-\sigma(z)).\]

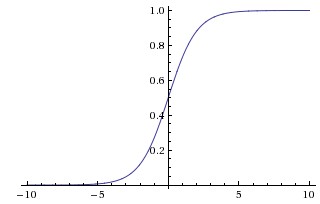
sigmoid 函数能够把输入的连续值压缩到 (0, 1) 范围内，其函数曲线如下：

../_images/02_sigmoid.jpeg

优点：

  • 单调连续，输出范围有限，优化稳定

  • 求导容易

缺点：

  • 容易饱和。当输入很大/很小时（Saturation, 饱和），神经元的梯度接近0，出现“梯度消失”（Gradient Vanishing），导致无法完成深层网络的训练。

  • 输出不是零均值的（Not Zero-centered）。假设某个神经元的输入一直是正的，即 \(x>0\) . 对于 \(f(x)=w^{\top} x + b\) ，则 \(w\) 获得的梯度将是恒正或者恒负 （取决于 \(f\) 得到的梯度的符号），导致 \(w\) 的更新非常“曲折”（Zig-Zagging）。 当然，如果是按 batch 训练，最终梯度是各个样本下梯度的和，而每个样本下的梯度可能是符号各异的，因此在一定程度上可以缓解这个问题。

6.2. tanh

tanh 函数的数学表达式如下：

\[tanh(z) = \frac{e^z-e^{-z}}{e^z+e^{-z}} = 2\sigma(2z)-1.\]

其函数曲线如下：

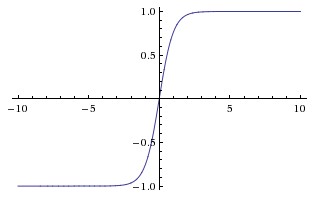
../_images/02_tanh.jpeg

与 sigmoid 一样， tanh 也会产生饱和现象，但是 tanh 的输出是零均值的（Zero-centered）。

6.3. relu

relu 函数的数学表达式如下：

\[relu(z) = max(0,z).\]

其函数曲线如下：

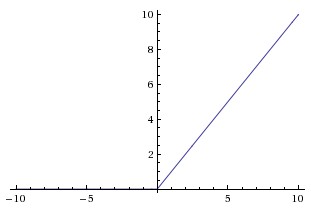
../_images/02_relu.jpeg

优点：

  • 避免梯度消失。

  • 计算简单。 sigmoid 和 tanh 都需要计算指数。

  • 收敛速度快。 Krizhevsky et al. 论文 指出 relu 收敛速度比 tanh 快6倍。

    ../_images/02_alexplot.jpeg

缺点:

  • 容易产生死亡节点（Dead ReLU）。一个非常大的梯度流过一个 relu 神经元，更新过参数之后，这个神经元对很多输入数据都输出0，则梯度一直为0。 当然 relu 的输出依靠 \(w\) 和 \(x\) 的共同作用，死亡节点可能会被重新激活。

  • 输出不是零均值的。

LeakyReLU 可以有效应对上述缺点。

6.4. softmax 与最大化对数似然

对数似然之外的许多目标函数对 softmax 单元不起作用。本质原因：若目标函数中不使用对数抵消 softmax 中的指数，当指数函数的变量取非常小的负值时， 会造成梯度消失，从而无法学习。

当 softmax 单元的输入值之间差异变得极端时，softmax 的输出会饱和，因此许多基于 softmax 的代价函数也会饱和，除非它们能够转换饱和的激活函数（例如，取对数）。 特别是平方误差，对 softmax 单元来说，它是一个很差的损失函数。

6.5. 梯度消失与梯度爆炸

梯度消失（Gradient Vanishing）：梯度太小，难以确定参数更新方向。解决策略：

  • 使用激活函数 relu（正部导数恒为 1）

  • Batch Normalization（将输出从饱和区拉到非饱和区）

  • 残差网络

  • LSTM（Long-Short Term Memory Networks）：遗忘门、输入门、输出门。

梯度爆炸（Gradient Exploding）：梯度太大，学习不稳定。解决策略：

  • 梯度截断（Gradient Clipping/Clamping）

  • 权重正则化

  • 使用激活函数 relu（正部导数恒为 1）

  • Batch Normalization（有正则化的作用）

6.6. 参考资料

  1. CS231n

  1. 神经网络之激活函数(Activation Function)

  1. What is the “dying ReLU” problem in neural networks?

  1. 详解机器学习中的梯度消失、爆炸原因及其解决方法