16. 几何

16.1. 仿射变换

仿射变换（Affine Transformation）是一个向量空间到另一个向量空间的变换（平移 + 线性变换），变换前后保持以下属性：

  • Collinearity ：共线的点仍然共线。

  • Parallelism ：平行的线仍然平行。

  • Convexity ：凸集仍然是凸集。

  • Ratios Of Lengths ：不同线段的长度比值保持不变。

  • Barycenters ：点集的重心保持不变。

$$ \begin{bmatrix} x^{\prime} \\ y^{\prime} \\ 1 \end{bmatrix} = T \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} ,\quad T = \begin{bmatrix} a_1 & a_2 & t_x \\ a_3 & a_4 & t_y \\ 0 & 0 & 1 \end{bmatrix} $$

恒等变换（Identity）

$$ T = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

平移（Translation）

$$ T = \begin{bmatrix} 1 & 0 & d_x \\ 0 & 1 & d_y \\ 0 & 0 & 1 \end{bmatrix} $$

缩放（Scaling）

$$ T = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

当 \(s_x=-1\) 或 \(s_y=-1\) 表示翻转（镜像）。

逆时针旋转（Rotation）

$$ T = \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

错切（Shear）

$$ T = \begin{bmatrix} 1 & sh_x & 0 \\ sh_y & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

16.2. 线段相交

问题 ：给定两条线段四个端点的坐标，判断两条线段是否相交。

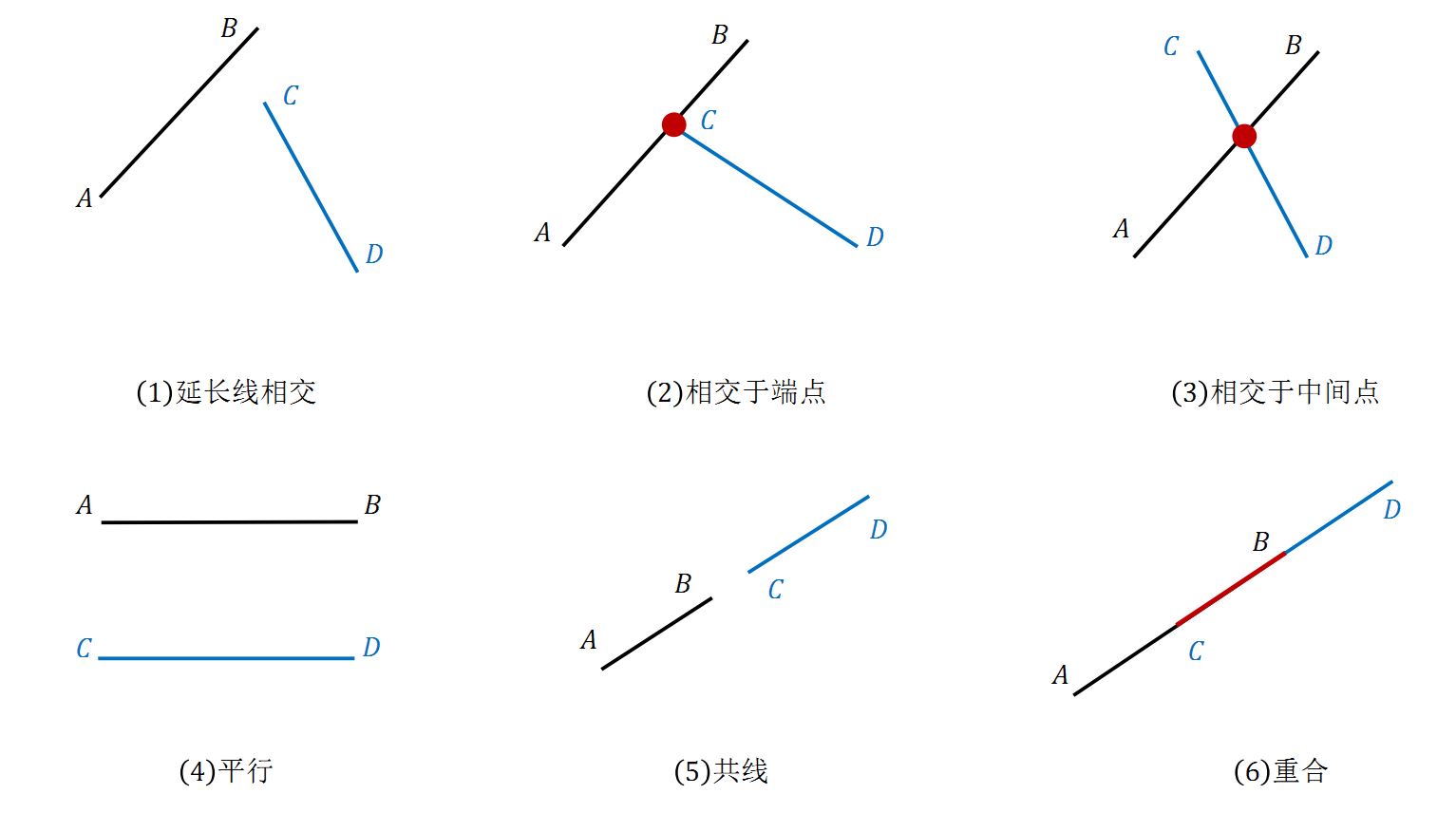
../_images/16_lineSegment.jpg

方法一：跨立实验

快速排斥

分别以两条线段为对角线作矩形，如果两个矩形没有重合部分（IoU = 0），则两条线段一定不相交。反之不然。

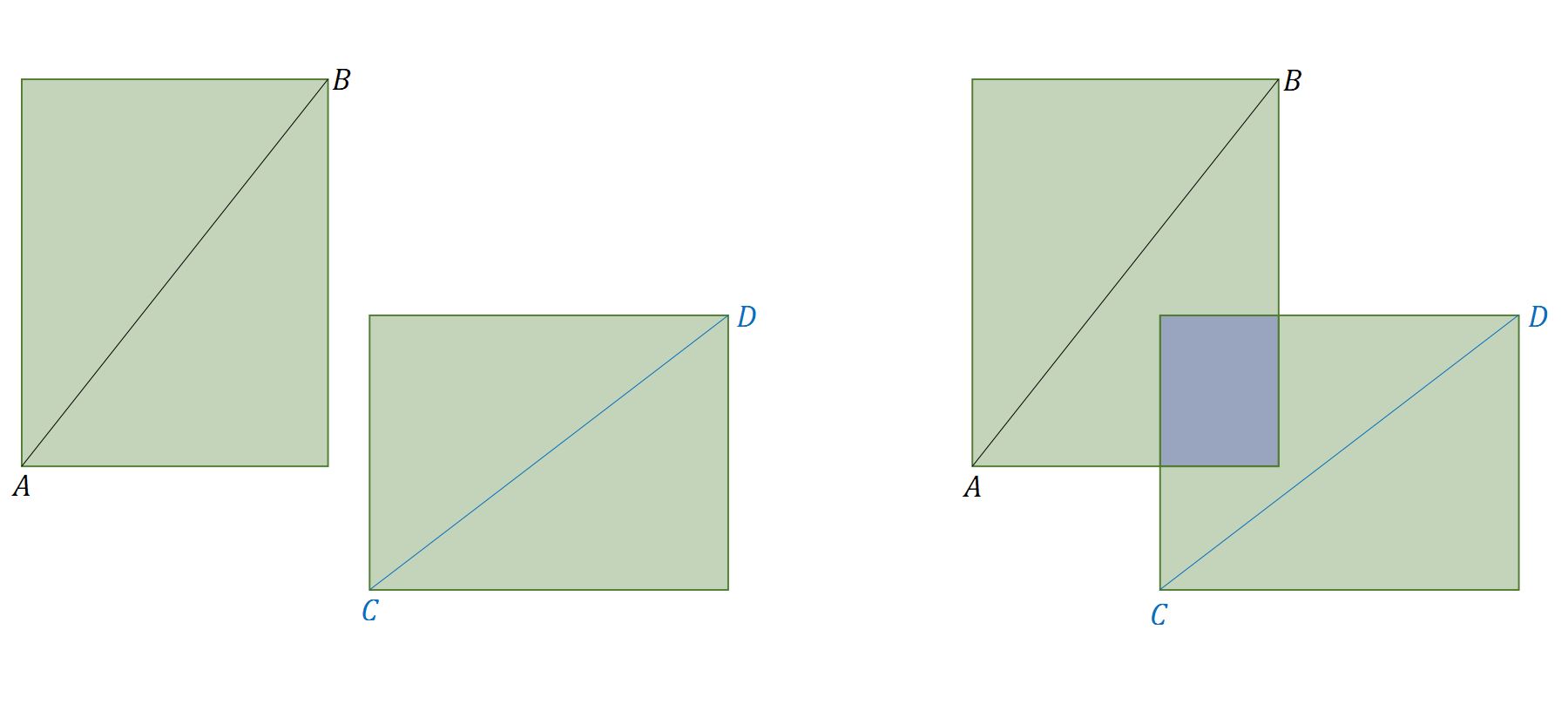
../_images/16_iou.jpg 
 1// 计算重合部分的顶点坐标，可用于计算 IoU
 2// rec = {x1, y1, x2, y2} 分别表示矩形左下角和右上角的顶点坐标
 3bool isRectangleOverlap(vector<int>& rec1, vector<int>& rec2)
 4{
 5    int left_x = max(rec1[0], rec2[0]);
 6    int right_x = min(rec1[2], rec2[2]);
 7    int bottom_y = max(rec1[1], rec2[1]);
 8    int top_y = min(rec1[3], rec2[3]);
 9    return (left_x < right_x && bottom_y < top_y);
10}

跨立实验

如果两条线段相交，那么：以其中任意一条线段为标准，另一条线段的两个端点一定在这条线段（延长线）的两端，或者在这条线段上。

如果在两端，利用向量叉乘（ Cross Product ）可表示为：

\[(\overrightarrow{AB} \times \overrightarrow{AC}) \cdot (\overrightarrow{AB} \times \overrightarrow{AD}) < 0,\quad (\overrightarrow{CD} \times \overrightarrow{CA}) \cdot (\overrightarrow{CD} \times \overrightarrow{CB}) < 0.\]
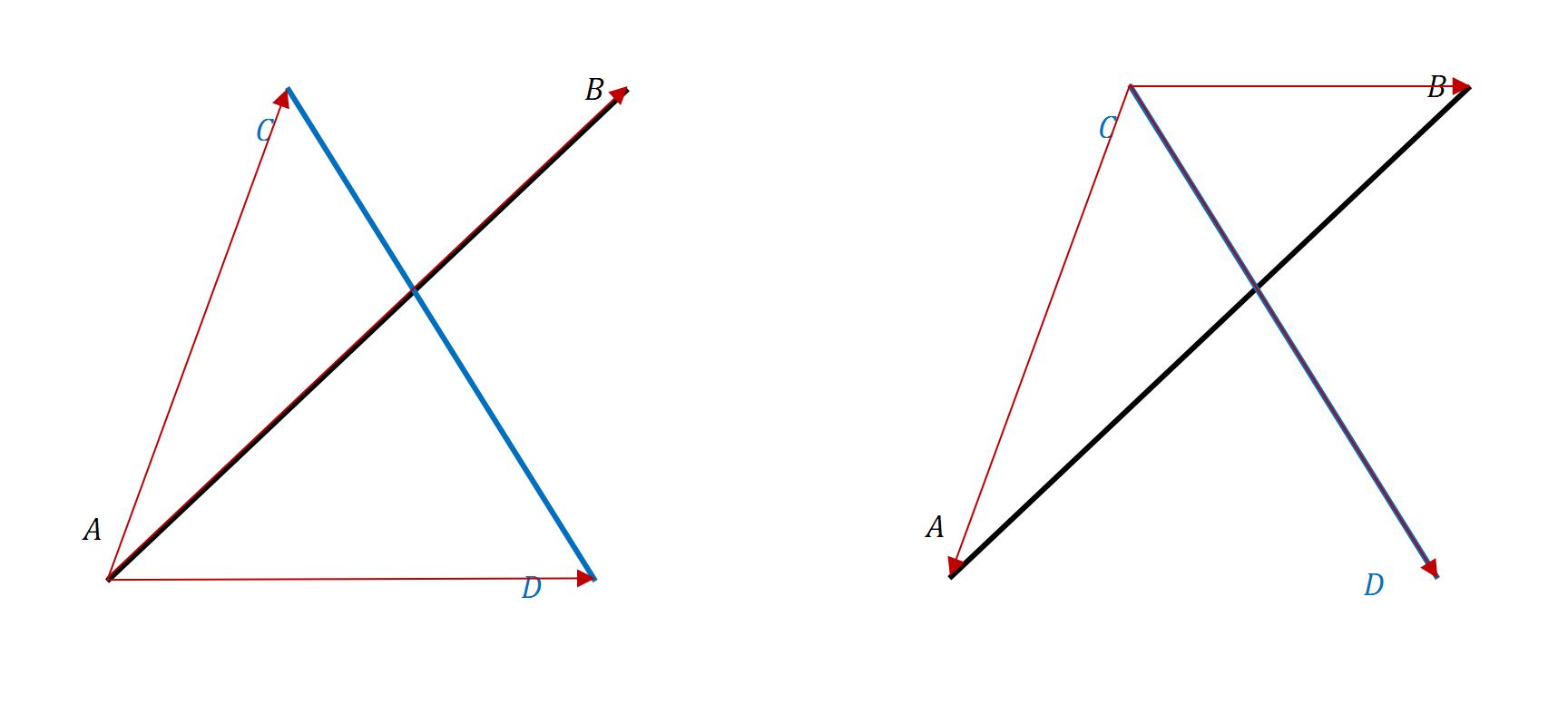
../_images/16_crossProduct.jpg
向量叉乘/向量积

两个向量 \(\vec{a},\vec{b}\) 的向量积 \(\vec{a} \times \vec{b}\) 为一个向量， 它的方向与 \(\vec{a},\vec{b}\) 都垂直，且使 \(\vec{a},\vec{b}, \vec{a} \times \vec{b}\) 构成右手系； 它的模等于以 \(\vec{a},\vec{b}\) 为边的平行四边形的面积，即 \(|\vec{a} \times \vec{b}| = |\vec{a}||\vec{b}|\sin \theta\) ， 其中 \(\theta\) 为 \(\vec{a},\vec{b}\) 的夹角。

性质：

\[\begin{split}\vec{a} \times \vec{b} &=\ - \vec{b} \times \vec{a} \\ \vec{a} \times \lambda \vec{a} &=\ 0\end{split}\]
$$ \vec{a} \times \vec{b} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} = \begin{vmatrix} a_2 & a_3\\ b_2 & b_3 \end{vmatrix} \vec{i} - \begin{vmatrix} a_1 & a_3\\ b_1 & b_3 \end{vmatrix} \vec{j} + \begin{vmatrix} a_1 & a_2\\ b_1 & b_2 \end{vmatrix} \vec{k} $$ $$ \begin{vmatrix} c_1 & c_2 \\ c_3 & c_4 \end{vmatrix} = c_1 c_4 - c_2 c_3 $$

其中 \([O; \vec{i}, \vec{j}, \vec{k}]\) 是一个直角坐标系；二维向量的第三维可扩展为 0。

相交判断

  • \((\overrightarrow{AB} \times \overrightarrow{AC}) \cdot (\overrightarrow{AB} \times \overrightarrow{AD}) > 0\) ： \(C\) 和 \(D\) 在线段 \(AB\) 的同一侧

    • 若 \((\overrightarrow{CD} \times \overrightarrow{CA}) \cdot (\overrightarrow{CD} \times \overrightarrow{CB}) = 0\) ， \(A\) 或 \(B\) 在线段 \(CD\) 的延长线上，不相交。

    • 若 \((\overrightarrow{CD} \times \overrightarrow{CA}) \cdot (\overrightarrow{CD} \times \overrightarrow{CB}) \neq 0\) ，不相交。

  • \((\overrightarrow{AB} \times \overrightarrow{AC}) \cdot (\overrightarrow{AB} \times \overrightarrow{AD}) < 0\) ： \(C\) 和 \(D\) 在线段 \(AB\) 的不同侧

    • 若 \((\overrightarrow{CD} \times \overrightarrow{CA}) \cdot (\overrightarrow{CD} \times \overrightarrow{CB}) \leqslant 0\) ，相交；如果等于 0，交点为 \(A\) 或 \(B\) 。

    • 若 \((\overrightarrow{CD} \times \overrightarrow{CA}) \cdot (\overrightarrow{CD} \times \overrightarrow{CB}) > 0\) ，不相交。

  • \((\overrightarrow{AB} \times \overrightarrow{AC}) \cdot (\overrightarrow{AB} \times \overrightarrow{AD}) = 0\) 可能是三种情形：

    • \(C\) 或 \(D\) 在线段 \(AB\) 上（交于 \(C\) 或 \(D\) ）。

    • \(C\) 或 \(D\) 在线段 \(AB\) 的延长线上（不相交），此时线段 \(CD\) 和线段 \(AB\) 可能是共线。

    • 线段 \(CD\) 和线段 \(AB\) 部分重合。

方法二：直线交点方程

\(AB\) 的直线方程：\(\overrightarrow{OA} + \lambda \overrightarrow{AB}\) ， \(CD\) 的直线方程：\(\overrightarrow{OC} + \mu \overrightarrow{CD}\) ，

即：

$$ \begin{cases} x &=\ x_a + \lambda (x_b - x_a) \\ y &=\ y_a + \lambda (y_b - y_a) \end{cases} $$ $$ \begin{cases} x &=\ x_c + \mu (x_d - x_c) \\ y &=\ y_c + \mu (y_d - y_c) \end{cases} $$

交点方程：

$$ \begin{cases} x_a + \lambda (x_b - x_a) &=\ x_c + \mu (x_d - x_c) \\ y_a + \lambda (y_b - y_a) &=\ y_c + \mu (y_d - y_c) \end{cases} $$

即：

$$ \begin{cases} \lambda (x_b - x_a) - \mu (x_d - x_c) &=\ x_c - x_a \\ \lambda (y_b - y_a) - \mu (y_d - y_c) &=\ y_c - y_a \end{cases} $$

若行列式

$$ \Delta = \begin{vmatrix} x_b - x_a & -(x_d - x_c) \\ y_b - y_a & -(y_d - y_c) \end{vmatrix} = 0 $$

表示两线段重合或平行。

若 \(\Delta \neq 0\) ，利用 Cramer 法则 求出：

$$ \lambda = \frac{1}{\Delta} \begin{vmatrix} x_c - x_a & -(x_d - x_c) \\ y_c - y_a & -(y_d - y_c) \end{vmatrix} $$ $$ \mu = \frac{1}{\Delta} \begin{vmatrix} x_b - x_a & x_c - x_a \\ y_b - y_a & y_c - y_a \end{vmatrix} $$

只有当 \(0 \leqslant \lambda \leqslant 1,\ 0 \leqslant \mu \leqslant 1\) 两条线段才相交，否则交点在线段的延长线上。

16.3. 凸多边形

问题 ：按逆时针顺序给定多边形 \(n\) 个顶点的坐标，判断该多边形是否是凸多边形。

方案 ：凸多边形的特点是：对于任意一条边，其他的边都在它的同一侧；按逆时针顺序，下一条边 \(\vec{l}_{i+1}\) 一定在当前边 \(\vec{l}_i\) 的逆时针方向。 判断方法：如果 \(\vec{l}_i \times \vec{l}_{i+1}\) 符号为正，则在逆时针方向；符号为负，则在顺时针方向；大小为 0，表示平行/共线。

16.4. 参考资料

  1. 计算几何-判断线段是否相交

  1. 线段的交点计算

  1. 何为仿射变换(Affine Transformation)

  1. Affine transformation