15. 概率基础
15.1. 贝叶斯公式
15.2. 全概率公式
15.3. 乘法定理
15.4. 事件独立
15.5. 容斥定理
集合:
概率:
15.6. 常见概率分布
分布 |
类型 |
概率密度函数(pdf) |
均值 |
方差 |
|---|---|---|---|---|
伯努利分布 |
离散 |
\(p^k (1-p)^{1-k},\ k \in \{ 0,1 \}\) |
\(p\) |
\(p(1-p)\) |
二项分布 |
离散 |
\(C_n^k p^k (1-p)^{n-k}\) |
\(np\) |
\(np(1-p)\) |
泊松分布 |
离散 |
\(\frac{\lambda^k}{k!}e^{-\lambda}\) |
\(\lambda\) |
\(\lambda\) |
均匀分布 |
连续 |
\(\frac{1}{b-a},\ a \leqslant x \leqslant b\) |
\(\frac{1}{2}(a+b)\) |
\(\frac{1}{12}(b-a)^2\) |
指数分布 |
连续 |
\(\lambda e^{-\lambda x},\ x \geqslant 0\) |
\(\frac{1}{\lambda}\) |
\(\frac{1}{\lambda ^2}\) |
正态分布 |
连续 |
\(\frac{1}{\sqrt{2 \pi} \sigma}\mathrm{exp}\left( -\frac{(x-\mu)^2}{2\sigma^2} \right)\) |
\(\mu\) |
\(\sigma^2\) |
对数正态分布 |
连续 |
\(\frac{1}{x}\cdot\frac{1}{\sqrt{2\pi}\sigma}\mathrm{exp}\left(-\frac{(\ln x-\mu)^2}{2\sigma^2} \right)\) |
\(e^{\mu + \frac{\sigma^2}{2}}\) |
\((e^{\sigma^2}-1)e^{2\mu + \sigma^2}\) |
拉普拉斯分布 |
连续 |
\(\frac{1}{2b}\mathrm{exp} \left( -\frac{|x - \mu|}{b} \right)\) |
\(\mu\) |
\(2b^2\) |
均值:
方差:
中位数:
众数:
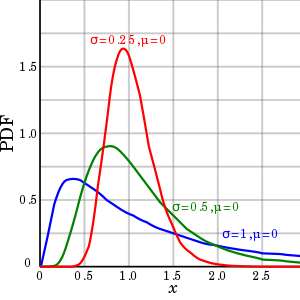
15.7. 对数正态分布
\(Y\) 服从标准正态分布,则 \(X = e^{\mu + \sigma Y}\) 服从对数正态分布: \(\ln (X) \sim \mathcal{N}(\mu, \sigma^2)\) 。
15.8. 实例
已知 \(X_1, X_2, ..., X_n\) 是 \(n\) 个相互独立同分布随机变量,\(F_X(x)\) 和 \(p_X(x)\) 是它们的(累计)分布函数和概率密度函数,分别求其最大值 \(Y = \mathrm{max}(X_1, X_2, ..., X_n)\) 与其最小值 \(Z = \mathrm{min}(X_1, X_2, ..., X_n)\) 的分布函数与概率密度函数。
- 解:
对于 \(Y\) :
\[\begin{split}F_Y(y) &=\ P(Y \leqslant y) \\ &=\ P(\mathrm{max}(X_1, X_2, ..., X_n) \leqslant y) \\ &=\ P(X_1 \leqslant y, X_2 \leqslant y, ..., X_n \leqslant y) \\ &=\ P(X_1 \leqslant y)P(X_2 \leqslant y) \cdots P(X_n \leqslant y) \\ &=\ [F_X(y)]^n\end{split}\]\[p_Y(y) = \frac{d}{dy} F_Y(y) = n [F_X(y)]^{n-1} p_X(y)\]对于 \(Z\) ,同理可得:
\[\begin{split}F_Z(z) &=\ P(Z \leqslant z) \\ &=\ 1 - P(Z \geqslant z) \\ &=\ 1 - P(X_1 \geqslant z, X_2 \geqslant z, ..., X_n \geqslant z) \\ &=\ 1 - [1 - F_X(z)]^n\end{split}\]\[p_Z(z) = \frac{d}{dz} F_Z(z) = n [1 - F_X(z)]^{n-1} p_X(z)\]例如,\(X_1, X_2, ..., X_n\) 均服从区间 \([0, 1]\) 的均匀分布,则 \(F_X(x) = x,\ p_X(x) = 1\) ,有
\[\begin{split}p_Y(y) = n y^{n-1},\ E[Y] = \frac{n}{n+1}; \\ p_Z(z) = n (1-z)^{n-1},\ E[Z] = \frac{1}{n+1}.\end{split}\]
设 \(X, Y\) 的联合概率密度函数为 \(f_{XY}(x, y)\) ,则 \(X+Y\) 的概率密度函数 \(f_Z(z) = \int_x f_{XY}(x, z-x) dx = \int_y f_{XY}(z-y, y) dy\) 。 若 \(X, Y \sim U(0, 1)\) 是相互独立的均匀分布,求 \(U = X + Y\) 和 \(V = X - Y\) 的概率密度函数。
- 解:
知 \(f_{XY}(x, y) = 1,\ x \in [0,1],\ y \in [0, 1]\) 。
对于 \(U\) ,
$$ f_U(u) = \int_{x \in [0,1],\ u-x \in [0,1]} f_{XY}(x, u-x) dx = \int_{\mathrm{max}(0, u-1)}^{\mathrm{min}(1, u)} f_{XY}(x, u-x) dx \\ = \begin{cases} u & , & 0 \leqslant u \leqslant 1 \\ 2 - u & , & 1 < u \leqslant 2 \end{cases} $$对于 \(V\) ,设 \(Z = -Y \sim U(-1, 0)\) ,则 \(V = X + Z\) ,
$$ f_V(v) = \int_{x \in [0,1],\ v-x \in [-1,0]} f_{XY}(x, v-x) dx = \int_{\mathrm{max}(0, v)}^{\mathrm{min}(1, v+1)} f_{XY}(x, v-x) dx \\ = \begin{cases} 1 + v & , & -1 \leqslant v \leqslant 0 \\ 1 - v & , & 0 < v \leqslant 1 \end{cases} $$
投掷一个均匀的硬币,求以下几种情况的期望投掷次数。
直到出现一次正面为止。
设投掷次数的期望为 \(e\) ,如果第一次投掷为正面,则投掷次数为 \(1\) ;否则平均投掷次数为 \(1 + e\) 。
\[e = \frac{1}{2} \times 1 + \frac{1}{2} \times (1 + e)\]解得 \(e = 2\) 。
直到出现两次正面为止(可以不连续)。
设投掷次数的期望为 \(E\) ,如果第一次投掷为正面,则平均投掷次数为 \(1 + e\) ( \(e = 2\) 为投出一次正面的期望次数);否则平均投掷次数为 \(1 + E\) 。
\[\begin{split}E = \frac{1}{2} \times (1 + e) + \frac{1}{2} \times (1 + E) \\\end{split}\]解得 \(E = 4\) 。
直到连续两次出现正面为止。
设投掷次数的期望为 \(E\) ,如果第一次投掷为反面,则平均投掷次数为 \(1 + E\) ;如果第一次投掷为正面,第二次投掷为反面,则平均投掷次数为 \(2 + E\) ;如果第一次和第二次投掷都为正面,则投掷次数为 \(2\) 。
\[\begin{split}E = \frac{1}{2} \times (1 + E) + \frac{1}{2} \times \frac{1}{2} \times (2 + E) + \frac{1}{2} \times \frac{1}{2} \times 2 \\\end{split}\]解得 \(E = 6\) 。
15.9. 参考资料
Inclusion–exclusion principle
Log-normal distribution